Cheat Sheets

Variable types

R basics

Basic operators + calculation

Operator Description Example
+ Add 3 + 4
- Subtract 10 - 8
* Multiply 6 * 32
/ Divide 100 / 25
^ Exponentiate 10 ^ 2
== Equals (logical) 10 == 10
<- Assign a value to a name ten <- 10

*See more logical operators here

Check data

Function Description Example
class() Check data type class(iris$Species)
ncol() Check number of columns ncol(iris)
nrow() Check number of rows nrow(iris)
head() Return first parts of an object head(iris)
tail() Return last parts of an object tail(iris)
str() Check data structure str(iris)
summary() Generate summary stats summary(iris)
levels() Return levels of a factor levels(iris$Species)

Create data

Function Description Example
c() Create a vector temp <- c("cool", "warm", "hot")
factor() Create a factor factor(temp)

Change data type

Function Description Example
as.numeric Treat as numeric as.numeric(temp)
as.factor Treat as factor as.factor(temp)
as.integer Treat as an integer as.integer(temp)

Make simple graphs

Function Description Example
hist() Create a histogram hist(iris$Petal.Width)
plot() Create an x-y plot plot(iris$Petal.Width ~ iris$Petal.Length)
boxplot() Create a boxplot boxplot(iris$Petal.Width ~ iris$Species)

Read + write data

Function Description Example
read.csv() Read a .csv file read.csv("file_name.csv")
write.csv() Write a .csv file write.csv(iris, "iris.csv")
getwd() Check the working directory getwd()

R Markdown

Graph

Grammar of graphics (ggplot2 package)

ggplot(data = penguins,                       # specify the dataset
       mapping = aes(x = flipper_length_mm,   # map a variable to the x axis 
                     y = body_mass_g,         # map a variable to the y axis 
                     color = species)) +      # map a grouping variable to color 
  geom_point()                                # choose shapes to represent data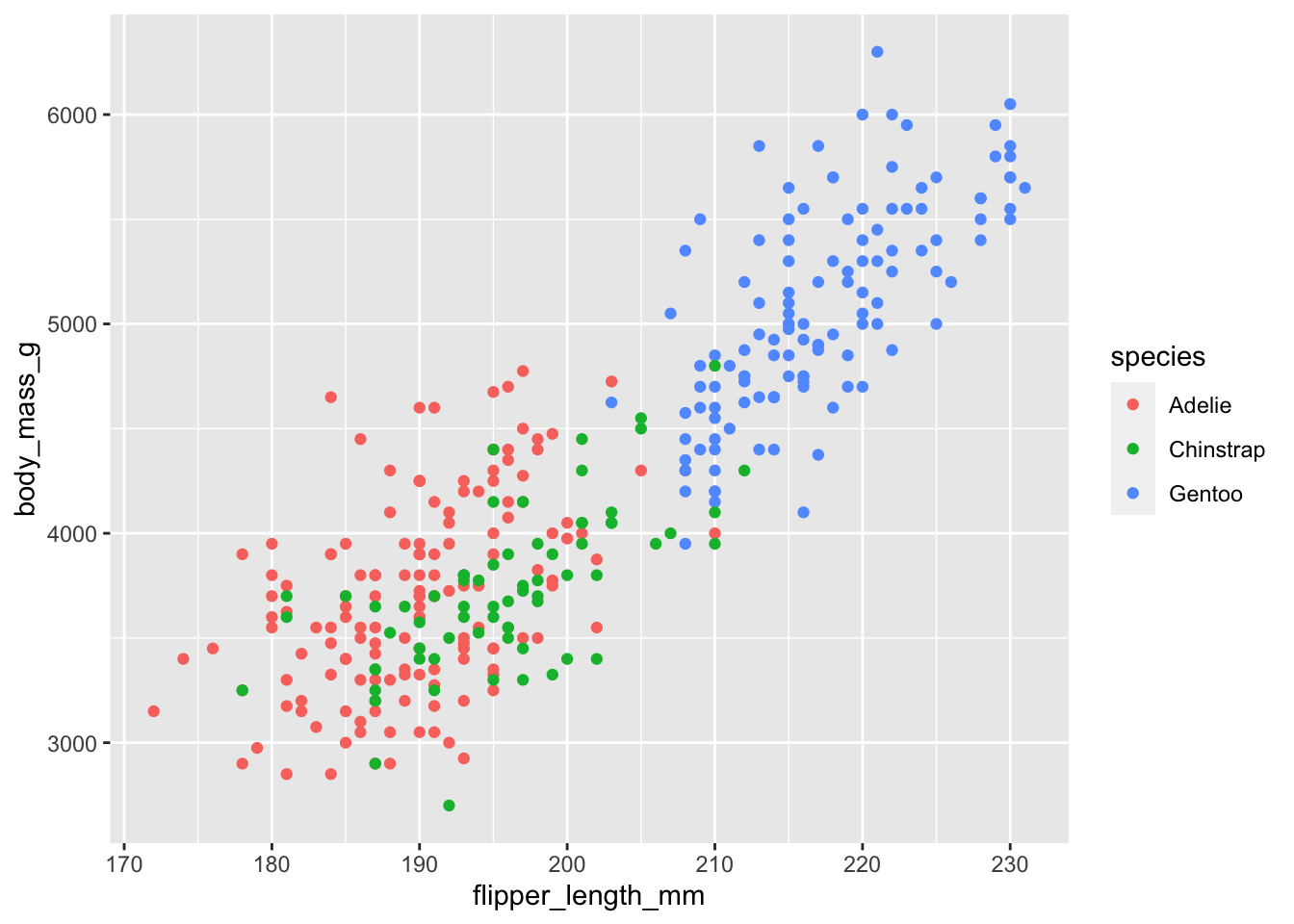

Version Author Date
c63d5b8 maggiedouglas 2024-04-16
88365b2 maggiedouglas 2024-02-08

Geom options

Function Description
geom_col() Make a barplot (sum)
geom_bar() Make a barplot (frequency/count)
geom_boxplot() Make a boxplot
geom_density() Make a density plot
geom_histogram() Make a histogram
geom_point() Make a scatterplot
geom_hline() Add a horizontal line to a plot (argument yintercept =)
geom_vline() Add a vertical line to a plot (argument xintercept =)

Common modifications

Function Description
xlim() Set the range of the x axis (arguments = numeric values for start + end)
ylim() Set the range of the y axis (arguments = numeric values for start + end)
xlab() Set the x axis label (needs to be in quotes)
ylab() Set the y axis label (needs to be in quotes)
theme() Adjust many aspects of graph appearance - fonts, gridlines, legends, etc.
theme_bw() Implement the theme ‘black and white’
theme_classic() Implement the theme ‘classic’

Additional resources

Wrangle

Work with packages

Function Description Example
install.packages() Install a package (needed only once) install.packages("tidyverse")
library() Load a package for use (every session) library(tidyverse)

Select + transform data (dplyr package)

Function Description
filter() Subset a data frame by condition
select() Select variables in a data frame
mutate() Create new variables
arrange() Order rows in a data frame

Tidy data (dplyr + tidyr packages)

Function Description
pivot_longer() Make a wide dataset long
pivot_wider() Make a long dataset wide

Additional resources

Summarize

Generate summary statistics (base R)

Function Description
sum() Add the values in a vector
mean() Calculate average of values in a vector
sd() Calculate the std deviation of values in a vector
length() Calculate length/# of elements of a vector = sample size
sqrt() Calcualte the square root of a value (needed for std error of the mean)

Aggregate or summarize by group (dplyr package)

Function Description
group_by() Set variable(s) to group a data frame
summarize() Generate summary values by the grouping variable(s) (e.g. mean = mean(x, na.rm=TRUE))
n() Calculate the sample size (# of rows) for each group

t-test

An outline of the steps involved in one-sample t-test:

1. Examine the suitability of data for a t-test

Check variable type to ensure Y is numeric. Helpful functions:

str()
class()
as.numeric() - encodes data as numeric as.factor() - encodes data as a (categorical) factor

2. Check the normality assumption

Visual inspection

Visualize the distribution of Y

ggplot(data = df, aes(y = Y) + geom_histogram()

OR

hist(df$Y)

Formal test

shapiro.test(df$Y)

  • P value < 0.05 means the data are NOT normal
  • P value > 0.05 means there is not strong enough evidence to reject the assumption of normality (use your judgement - in combination with the visual inspection)

3. Transform if needed

Two common transformations:

Square root: sqrt(df$Y)
Log base 10: log10(df$Y)

  • You can also use mutate with these functions to store the transformed variable in the data frame

4. Run the test

Meets normality assumption

Standard t-test example:

t.test(df$Y, alternative = "two.sided", mu = 3, conf.level = 0.95)

  • Tests whether the mean of the population of variable Y is significantly different than some value (mu = 3 in this example)
  • Two-sided means that it tests both greater and less than the value of mu
  • Set to return a 95% confidence interval
Violates the normality assumption

Wilcoxon signed rank test example:

wilcox.test(df$Y, alternative = "two.sided", mu = 3, conf.int = TRUE, conf.level = 0.95)

  • Tests whether the median of the population of variable Y is significantly different than some value (mu = 3 in this example)
  • Two-sided means that it tests both greater and less than the value of mu
  • Set to return a 95% confidence interval

Regression

An outline of the steps involved in linear regression…

See also example code for more detail

1. Assess suitability for linear regression

Are the variables numeric?

Check variable types to ensure X and Y are numeric variables. Helpful functions:

str()
class()
as.numeric()

Are the data points independent?

Remember to ‘check your n’s’ to see how many data points are in the dataset.

What does a row represent?

Is it reasonable to assume that the data points are independent of one another?

What do you know about the experimental design?

Is the relationship linear?

Examine the shape of relationship between X and Y

ggplot(data = df, aes(x = X, y = Y) + geom_point()

OR

plot(df$Y ~ df$X)

What to do if basic requirements are violated:
  • Independence
    • If it is a borderline case, use visual diagnostics to assess whether related points are clustered (if not, you are probably okay)
    • Consider aggregating (e.g. taking a mean across groups) so that you have fewer observations that are independent
    • Worst case, you may need to conclude that regression is not appropriate given the experimental design!
  • Linearity
    • If there simply does not seem to be any relationship, you can still use linear regression and it will likely confirm that there is no relationship between variables.
    • If the relationship looks exponential or otherwise curved, it may be possible to transform X, Y, or both to make it linear.
    • If there is a more complex curved relationship (e.g. a U shape or hump shape), ideally you would explore non-linear regression methods (e.g. adding an X2 term, called a quadratic model).

2. Fit the model

Using the function lm()…

mod <- lm(Y ~ X, data = df)

3. Check normality and equal variance assumptions

Check for normality + equal variance of residuals:

plot(mod)

Another check for normality of residuals:

hist(mod$residuals)

Here is a resource on interpreting residual plots

Here is a resource on interpreting leverage plots

4. What to do if normality/equal variance assumptions are violated

Option 1: Transform variables to meet assumptions

This is an option when the residuals and/or underlying variables have skewed distributions. The outcomes are easier to interpret for a log transform than a square root transform. It is most common to transform the X variable, but there are situations where it makes sense to transform Y or X and Y.

Natural log: log(df$X)

Log base 10: log10(df$X)

Square root: sqrt(df$X)

  • You can also use mutate for these operations to store the variable in the dataset

Fit + evaluate the new model on transformed variables… (return to #2 + #3, making sure to fit the model under a new name so you can compare diagnostics/outputs for each)

Option 2: Remove outliers (if outliers are driving the issue)

This is an option if there are a few unusual observations that are far outside the pattern of the rest of the data, and have a heavy influence on fitting the regression line. Outliers will be marked in the residual plots. Their influence on the regression can be assessed using the residuals vs. leverage plot.

Remove outliers (e.g. remove rows # 1, 2, 3)

df_no_out <- df[-c(1,2,3),]

Here is a resource on indexing

Alternatively, you can add a column to your dataset identifying outliers using mutate and ifelse.

See example code - Example 1

Fit + evaluate a new model if needed… (return to #2 + #3, making sure to fit the model under a new name so you can compare diagnostics/outputs for each)

Option 3: Fit a non-parametric model (Theil-Sen regression)

This is an option if transformation fails to help the data meet assumptions. This method is also not very sensitive to outliers, so it is an alternative to removing them. Keep in mind that this method still assumes linearity and independence.

Using the function mblm()… in the package mblm

mod <- mblm(Y ~ X, data = df)

Important note!

The function mblm does not work if there are NA values in X or Y. To solve this problem you can use the drop_na() function to remove NA values before fitting the model:

df_no_NA <- df %>% select(X, Y) %>% drop_na()

Then you would fit:

mod <- mblm(Y ~ X, data = df_no_NA)

5. Interpret + graph results

Generate model summary

summary(mod)

Key aspects of the output include:

  • The model P value (Is there a linear relationship between X and Y?)
  • The adjusted R2 value (How strong is the relationship? How much variation in Y can X explain?)
  • The estimates for the intercept and slope (What line best represents the relationship between X and Y? How much does Y change for a 1-unit change in X?)
Make a final plot with a trend line

ggplot(data = df, aes(x = X, y = Y)) +
geom_point() +

Trend line for standard regression with 95% confidence interval around the slope:

geom_smooth(method = "lm", se = TRUE)

Trend line for log10-transformed X with 95% confidence interval around the slope:

geom_smooth(method = "lm", formula = 'y ~ log10(x)', se = TRUE)

Trend line for Theil-Sen regression:

geom_abline(intercept = coef(mod)[1], slope = coef(mod)[2], color = "blue")

ANOVA

An outline of the steps involved in one-way ANOVA…

See also example code for more detail

1. Examine suitability of data for ANOVA

Check variable types to ensure X is categorical and Y is numeric. Helpful functions:

str()
class()
as.numeric() as.factor() - encodes data as a (categorical) factor

Examine the distributions of X and Y

ggplot(data = df, aes(x = X) + geom_histogram()

OR

hist(df$X)

Examine the distribution of Y by X grouping variable

ggplot(data = df, aes(x = X, y = Y) + geom_boxplot()

OR

boxplot(df$Y ~ df$X)

Note: If you get an error with boxplot, you may have NA values in your data that are causing problems. At the start of your code where you are preparing the data, you can remove them using the function drop_na().

2. Fit the model

Using the function aov()…

mod <- aov(Y ~ X, data = df)

3. Check assumptions

Check for normality + equal variance of residuals:

plot(mod)

Another check for normality of residuals:

hist(mod$residuals)

Another check for equal variance among groups:

boxplot(mod$residuals ~ df$X)

4. Adjust if needed

Consider your options…

  • Non-normal residuals: Consider transforming the Y variable
  • Unequal variance: Consider Welch’s ANOVA
  • Non-normal residuals + unequal variance: Start with transformation, then go from there…
Transform the variable(s)

Log base 10: log10(df$X)
Square root: sqrt(df$X)

  • You can also use mutate to store the outcome of these operations as a new variable

Fit + evaluate (return to #2 + #3, making sure to fit the model under a new name so you can compare diagnostics/outputs for each)

Welch’s ANOVA

Does not assume equal variance.

oneway.test(Y ~ X, data = df)

Removing outliers (last resort)

e.g. remove rows # 1, 2, 3

df_no_out <- df[-c(1,2,3),]

Here is a resource on indexing

5. Interpret results

Standard ANOVA

Generate model summary:

anova(mod)

If significant differences are present, generate post-hoc comparisons of groups:

HSD.test(mod, "X", group = TRUE, console = TRUE, unbalanced = TRUE) (in package agricolae)

Note: The argument unbalanced should be set to TRUE if the sample size is unequal across groups. If y

Welch’s ANOVA

Generate model summary:

mod

If significant differences are present, generate post-hoc comparisons of groups:

games_howell_test(Y ~ X, data = df)

6. Graph results

Make a final plot with error bars. If you transformed the data, be sure to use the back-transformed means and standard errors.

See example code at the end of the script here.

Spatial data

Key spatial packages

  • sp: spatial object definitions + some methods
  • sf: will replace sp eventually; spatial object definitions + methods
  • raster: work with raster data, many processing functions
  • spdep: analysis tools for spatial data
  • tmap: visualization of vector and raster images
  • rasterVis: visualization of rater images
  • RColorBrewer: helpful package to generate/apply color scales

Resources + guides

sf (spatial object definitions + some methods)
sp (spatial object defintions + some methods, to be replaced by sf)
usmap (US political boundaries)
RColorBrewer (create color scales)
Further reading/resources

sessionInfo()
R version 4.3.2 (2023-10-31)
Platform: x86_64-apple-darwin20 (64-bit)
Running under: macOS Monterey 12.4

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.3-x86_64/Resources/lib/libRblas.0.dylib 
LAPACK: /Library/Frameworks/R.framework/Versions/4.3-x86_64/Resources/lib/libRlapack.dylib;  LAPACK version 3.11.0

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

time zone: America/New_York
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
 [1] palmerpenguins_0.1.1 lubridate_1.9.3      forcats_1.0.0       
 [4] stringr_1.5.1        dplyr_1.1.4          purrr_1.0.2         
 [7] readr_2.1.5          tidyr_1.3.0          tibble_3.2.1        
[10] ggplot2_3.4.4        tidyverse_2.0.0      DiagrammeR_1.0.10   

loaded via a namespace (and not attached):
 [1] sass_0.4.8         utf8_1.2.4         generics_0.1.3     stringi_1.8.3     
 [5] hms_1.1.3          digest_0.6.34      magrittr_2.0.3     timechange_0.3.0  
 [9] evaluate_0.23      grid_4.3.2         RColorBrewer_1.1-3 fastmap_1.1.1     
[13] rprojroot_2.0.4    workflowr_1.7.1    jsonlite_1.8.8     whisker_0.4.1     
[17] promises_1.2.1     fansi_1.0.6        scales_1.3.0       jquerylib_0.1.4   
[21] cli_3.6.2          rlang_1.1.3        visNetwork_2.1.2   ellipsis_0.3.2    
[25] munsell_0.5.0      withr_3.0.0        cachem_1.0.8       yaml_2.3.8        
[29] tools_4.3.2        tzdb_0.4.0         colorspace_2.1-0   httpuv_1.6.13     
[33] vctrs_0.6.5        R6_2.5.1           lifecycle_1.0.4    git2r_0.33.0      
[37] fs_1.6.3           htmlwidgets_1.6.4  pkgconfig_2.0.3    pillar_1.9.0      
[41] bslib_0.6.1        later_1.3.2        gtable_0.3.4       glue_1.7.0        
[45] Rcpp_1.0.12        highr_0.10         xfun_0.41          tidyselect_1.2.0  
[49] rstudioapi_0.15.0  knitr_1.45         farver_2.1.1       htmltools_0.5.7   
[53] labeling_0.4.3     rmarkdown_2.25     compiler_4.3.2